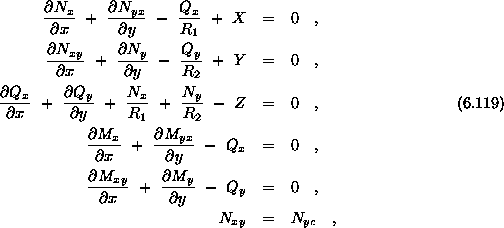
Diferencialne enačbe lupin so izpeljane iz ravnotežnih pogojev diferencialno majhnega elementa. Ker je v platišču prisoten tudi upogibni moment je potrebno uporabit upogibno terijo lupin. Nastaviti je potrebno tri ravnotežne enačbe v smereh koordinatnih osi x, y in z za kartezijev koordinatni sistem ali cirkularni in meridianski smeri ter v smeri normale na lupino če se enačbe izpeljujejo v cilindrične koordinatnem sistemu. Pri upoštevanju membranske teorije, na delec delujejo normalne sile, prečne sile ter upogibni momenti. Iz ravnotežnih pogojev sil na delec slede ravnotežne enačbe
kjer so X, Y in Z komponenete zunanjih sil pomen ostalih oznak
pa je razviden iz slike 
.
To so poenostavljene enačbe v katerih je
Pri MKE se izkaže ta pogoj kot zadovoljiv, če je krivinski radij elementa predpostavljen kot konstantna vrednost. Ko stranice elementa ali robne tangencialne sile niso paralelne (med seboj), temveč obstaja med njimi kot različen od nič, potem te sile dajo normalno komponento
kjer je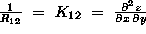 
kombinirana
ukrivljenost površine lupine. Ta komponenta se prišteje tretji
enačbi v ().
Vse obremenitve v () sa dajo izraziti s pomočjo
pomikov u, v in w ter njihovimi odvodi v smereh koordinatnih
osi x, y in z. S substitucijo obremenitev v ()
z odgovarjajočimi , v teoriji elastičnosti definiranimi
, relacijami, ki vpeljejo pomike ter njihove odvode se problem zreducira
na sistem treh parcialnih diferencialnih enačb
Prvi dve enačbi predstavljata ravnotežje obremenitev v smereh x in
y in sta ekvivalentni enačbam ravninskega napetostnega stanja. V
njiuju nastopata še dodatni tangencialni sili zaradi normalnih
pomikov v smerei w, predstavljeni z zadnjim členom v obeg
enačbah. Tretja enačba v () predstavlja ravnotežje
obremenitev v smeri normale na površino. Zadnji člen leve strani te
enačbe predstavlja diferencialno enačbo upogiba plošče. Normalna
komponenta sile (), zaradi kombiniranega krivinskega
radija izražena s pomiki je
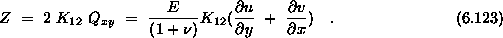
Ta normalna sila mora biti vsebovana v tretji enačbi ()
