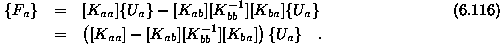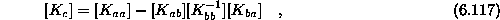

Naprej: Računanje lupin z
Gor: Splošen postopek MKE
Nazaj: Zunanja obremenitev
Vsebina: 
S togostno matriko elementa 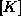 ali togostno matriko konstrukcije
ali togostno matriko konstrukcije
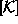 se povežejo vse sile in pomiki obravnavane konstrukcije. Ponekod
ne želimo obravnavati vseh sil. Obravnavamo samo bistvene sile in momente. V
takih primerih je potrebno izračunati novo togostno matriko, ki zajema samo
bistvene sile in momente s tem pa bo zajela samo nekatere prostostne stopnje
vektorja pomika. Takšno togostno matriko imenujemo kondenzirana togostna
matrika. Potreba po uvedbi kondenzirane togostne matrike nastopi pri mešanih
konstrukcija. Vzemimo naprimer stičišče nosilca v ravnini, ki ima v vsakem
vozlišču tri prostostne stopnje (osno, prečno silo in upogibni moment) ter
ploskovnega elementa, ki ima v vsakem vozlišču dve prostostni stopnji.
V tem primeru je potrebno vozliščem ob stiku stene z nosilcem, prirediti
vektorje enakega ranga.
se povežejo vse sile in pomiki obravnavane konstrukcije. Ponekod
ne želimo obravnavati vseh sil. Obravnavamo samo bistvene sile in momente. V
takih primerih je potrebno izračunati novo togostno matriko, ki zajema samo
bistvene sile in momente s tem pa bo zajela samo nekatere prostostne stopnje
vektorja pomika. Takšno togostno matriko imenujemo kondenzirana togostna
matrika. Potreba po uvedbi kondenzirane togostne matrike nastopi pri mešanih
konstrukcija. Vzemimo naprimer stičišče nosilca v ravnini, ki ima v vsakem
vozlišču tri prostostne stopnje (osno, prečno silo in upogibni moment) ter
ploskovnega elementa, ki ima v vsakem vozlišču dve prostostni stopnji.
V tem primeru je potrebno vozliščem ob stiku stene z nosilcem, prirediti
vektorje enakega ranga.
Bistvene robne pogoje imenujmo a in nebistvene b. Enačbo
prizadetega elementa parcioniramo v obliko
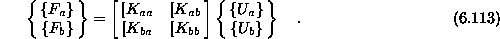
Pri predpodstavki da je vektor nepomemnbih sil 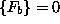 sledi iz durge
enačbe
sledi iz durge
enačbe
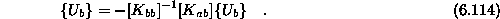
Zadnja enačbo je možno zapisati pod pogojem, da je 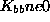 Če v prvo enačbo
Če v prvo enačbo
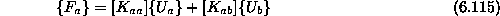
vstavimo 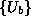 je
je
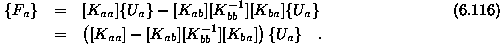
Pišemo krajše z matriko
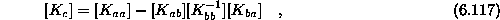
ki jo imenujemo kondenzirana togostna matrika tako je

Leon Kos
Mon Apr 22 10:36:01 GMT+0100 1996
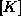 ali togostno matriko konstrukcije
ali togostno matriko konstrukcije
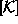 se povežejo vse sile in pomiki obravnavane konstrukcije. Ponekod
ne želimo obravnavati vseh sil. Obravnavamo samo bistvene sile in momente. V
takih primerih je potrebno izračunati novo togostno matriko, ki zajema samo
bistvene sile in momente s tem pa bo zajela samo nekatere prostostne stopnje
vektorja pomika. Takšno togostno matriko imenujemo kondenzirana togostna
matrika. Potreba po uvedbi kondenzirane togostne matrike nastopi pri mešanih
konstrukcija. Vzemimo naprimer stičišče nosilca v ravnini, ki ima v vsakem
vozlišču tri prostostne stopnje (osno, prečno silo in upogibni moment) ter
ploskovnega elementa, ki ima v vsakem vozlišču dve prostostni stopnji.
V tem primeru je potrebno vozliščem ob stiku stene z nosilcem, prirediti
vektorje enakega ranga.
se povežejo vse sile in pomiki obravnavane konstrukcije. Ponekod
ne želimo obravnavati vseh sil. Obravnavamo samo bistvene sile in momente. V
takih primerih je potrebno izračunati novo togostno matriko, ki zajema samo
bistvene sile in momente s tem pa bo zajela samo nekatere prostostne stopnje
vektorja pomika. Takšno togostno matriko imenujemo kondenzirana togostna
matrika. Potreba po uvedbi kondenzirane togostne matrike nastopi pri mešanih
konstrukcija. Vzemimo naprimer stičišče nosilca v ravnini, ki ima v vsakem
vozlišču tri prostostne stopnje (osno, prečno silo in upogibni moment) ter
ploskovnega elementa, ki ima v vsakem vozlišču dve prostostni stopnji.
V tem primeru je potrebno vozliščem ob stiku stene z nosilcem, prirediti
vektorje enakega ranga.
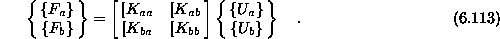
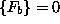 sledi iz durge
enačbe
sledi iz durge
enačbe
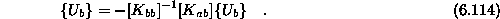
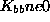 Če v prvo enačbo
Če v prvo enačbo
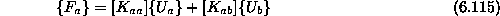
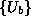 je
je